Research

My research lies in the interface of machine learning/non-parametric statistics, applied probability and numerical computation, with a primary focus on the algorithmic and theoretical foundations for solving model based/informed data-driven problems.

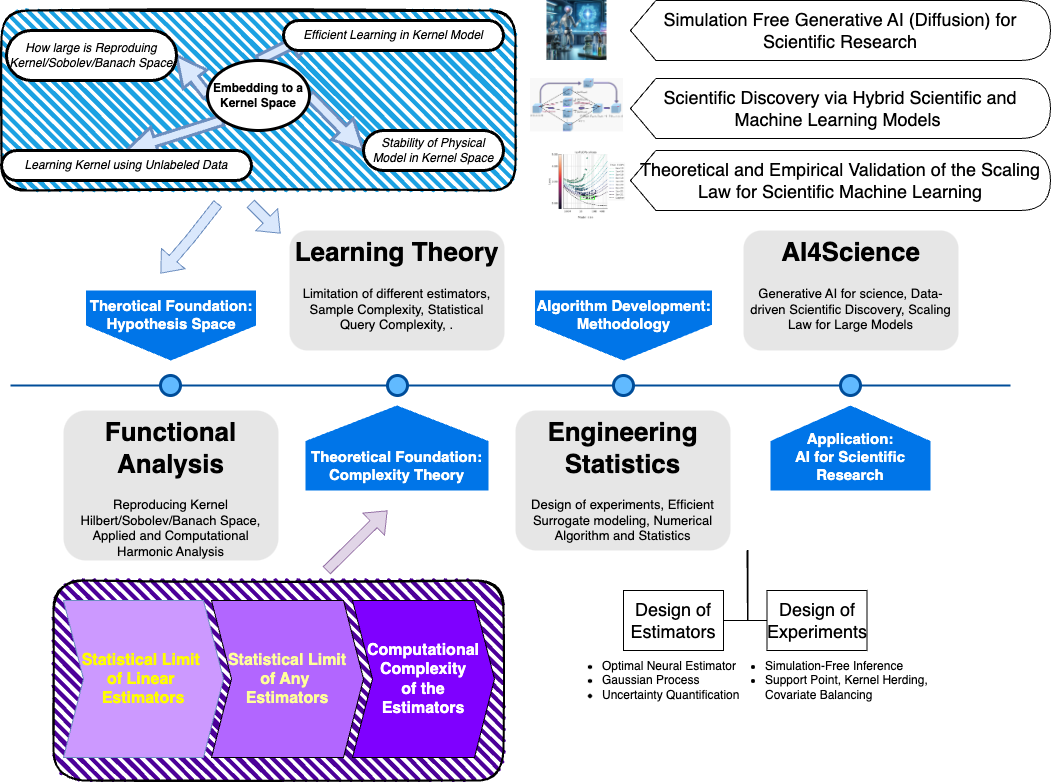
Scientific Machine Learning/Machine Learning for Science

Validated Scientific Machine Learning via Debiasing

Coming soon, here’s our first paper on theory

Sample Complexity and Optimization of Scientific Machine Learning

How large the sample size and how much computational power are needed to reach a prescribed performance level for a physic problem?

• ML Solving PDE: In a ICLR 2022 paper, we analysis the sample complexity of learning a PDE solution and show a suboptimality of plug-in solvers. In a Neurips 2022 paper, we analysis the optimization dynamic and show that using Sobolev norm as loss function can accelerate neural network training.

• Operator Learning: In a ICLR 2023 paper , we consider the optimal learning rate for learning a linear operator between two infinite dimensional Hilbert spaces. We provided a novel lower bound to the literature and showed that multi-level machine learning is essential to achieve an optimal learning rate. This example showed a fundamental difference between infinite dimension machine learning and finite dimension one both in sample complexity and algorithmic design.

Encoding Physics Information into a Model

• In a ICML 2018 paper, we present an initial attempt to learn evolution PDEs from data. The proposed PDE-Net learns differential operators by learning convolution kernels (filters) as finite difference scheme and apply neural networks or other machine learning methods to approximate the unknown nonlinear responses. This approach combines the representation power of the deep neural networks and the transparency of the PDE models which lead to better generalization property towards diverse initial conditions.

• In another ICML 2018 paper, we contributed to the understanding of popular neural networks by interpreting them as different numerical discretizations of (stochastic) differential equations. Our work is among the first to explore this relationship between ResNet and ODE.

• In a Neurips 2019 paper and a ICML 2020 paper, we further advanced the understanding of neural networks by linking their training process to solving an optimal control problem. This perspective offers both theoretical and empirical benefits in improving our ability to train neural networks effectively.

Robust Machine Learning

• In a ICLR 2022 paper, we analyze Neural Collapse (NC), a highly symmetric geometry of neural networks that emerges during the terminal phase of training which leads to better generalization performance, better robustness, and better interpretability. We show that NC can be understood from a large margin view point. In a arXiv paper, we use NC as a tool to improve overparametrized model trained with unlabel data.

• In a Neurips 2019 paper, we accelerated adversarial training by 3-5 times.

Experiment Design

Balanced Experiment Design: In this arxiv paper, we surprisingly connect balanced experiment design for panel data with phase retrieval problem from the inverse problem community. This connection enables us to generate the design via a generalized power method. For economists, our paper discovered that best experiment = smallest (nonlinear) eigenvector for the smallest eigenvector can cancel most linear effects.

Other Projects

• Inverse Problem and Image Processing: Image inpainting via manifold learning [SIIMS paper], Control Inspired NN based Image Editting [ICLR 2019 paper]